2023/12/6最新更新专利技术
-
.本发明涉及防腐剂领域,具体涉及一种具有高效抗氧化抑菌效果的组合物及其应用。.从农场到餐桌的整个环节中,食品均易受到微生物的侵染而发生腐败。全球每年约有.亿吨的食物因食品腐败被浪费,约占总生产产出的三分之一。化学防腐剂有低毒性和引起细菌耐药性的风险,故寻找安全的天然食品原料作为抑菌抗氧化进...
-
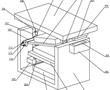
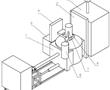
.本发明涉及激光校靶,尤其是指一种基于激光校准用自定位目标靶装置。.激光校靶作为发射轴线与瞄准轴线一致性检测方式已被广泛使用,其工作原理:利用激光相干性和准直性好的特点,以激光作为发射轴线的理论延长线,激光光斑中心对准目标位置(发射轴线与靶板相交点),调整瞄准镜,使瞄准镜中心对准瞄...
-
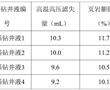
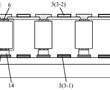
.本发明涉及航空发动机高温合金定向/单晶铸件的熔模铸造,具体涉及一种定向/单晶高温合金铸件熔模铸造用惰性陶瓷型壳制备方法。.定向/单晶铸件熔模铸造浇注过程中,℃左右的高温合金液要在型壳中停留至少h,合金熔体中的活泼元素与型壳内腔表面易发生复杂的物理、化学相互作用,当物理、化学反应过...
-
.本发明涉及医用硅胶带,具体为一种医用硅胶胶带及其制备方法。.硅胶胶带是医院中常用的物品,但现有的硅胶胶带仍然存在不足之处,具体为:现有的硅胶胶带透气性较差,容易刺激皮肤,影响患者伤口愈合。.因此,需要一种医用硅胶胶带及其制备方法来解决上述中提出的问题。发明内容.本发明的目...
利记sbobet网址
- 农业,林业,园林,畜牧业,肥料饲料的机械,工具制造及其应用技术
- 食品,饮料机械,设备的制造及其制品加工制作,储藏技术
- 烟草加工设备的制造及烟草加工技术
- 服装,鞋;帽,珠宝,饰品制造的工具及其制品制作技术
- 医药医疗技术的改进;医疗器械制造及应用技术
- 家居日用产品装置的制造及产品制作技术
- 休闲,运动,玩具,娱乐用品的装置及其制品制造技术
- 木材加工工具,设备的制造及其制品制作技术
- 纺织,织造,皮革制品制作工具,设备的制造及其制品技术处理方法
- 建筑材料工具的制造及其制品处理技术
- 家具;门窗制品及其配附件制造技术
- 水利;给水;排水工程装置的制造及其处理技术
- 道路,铁路或桥梁建设机械的制造及建造技术
- 五金工具产品及配附件制造技术
- 安全;消防;救生装置及其产品制造技术
- 造纸;纤维素;纸品设备的制造及其加工制造技术
- 印刷排版;打字模印装置的制造及其产品制作工艺
- 办公文教;装订;广告设备的制造及其产品制作工艺
- 工艺制品设备的制造及其制作,处理技术
- 摄影电影;光学设备的制造及其处理,应用技术
- 乐器;声学设备的制造及制作,分析技术
- 照明工业产品的制造及其应用技术
- 机械加工,机床金属加工设备的制造及其加工,应用技术
- 金属材料;冶金;铸造;磨削;抛光设备的制造及处理,应用技术
- 无机化学及其化合物制造及其合成,应用技术
- 有机化学装置的制造及其处理,应用技术
- 有机化合物处理,合成应用技术
- 喷涂装置;染料;涂料;抛光剂;天然树脂;黏合剂装置的制造及其制作,应用技术
- 车辆装置的制造及其改造技术
- 铁路车辆辅助装置的制造及其改造技术
- 自行车,非机动车装置制造技术
- 船舶设备制造技术
- 航空航天装置制造技术
- 包装,储藏,运输设备的制造及其应用技术
- 塑料加工应用技术
- 蒸汽制造应用技术
- 燃烧设备;加热装置的制造及其应用技术
- 供热;炉灶;通风;干燥设备的制造及其应用技术
- 制冷或冷却;气体的液化或固化装置的制造及其应用技术
- 环保节能,再生,污水处理设备的制造及其应用技术
- 物理化学装置的制造及其应用技术
- 分离筛选设备的制造及其应用技术
- 石油,煤气及炼焦工业设备的制造及其应用技术
- 发动机及配件附件的制造及其应用技术
- 微观装置的制造及其处理技术
- 电解或电泳工艺的制造及其应用技术
- 土层或岩石的钻进;采矿的设备制造及其应用技术
- 非变容式泵设备的制造及其应用技术
- 流体压力执行机构;一般液压技术和气动零部件的制造及其应用技术
- 工程元件,部件;绝热;紧固件装置的制造及其应用技术
- 气体或液体的贮存或分配装置的制造及其应用技术
- 测量装置的制造及其应用技术
- 测时;钟表制品的制造及其维修技术
- 控制;调节装置的制造及其应用技术
- 计算;推算;计数设备的制造及其应用技术
- 核算装置的制造及其应用技术
- 信号装置的制造及其应用技术
- 信息存储应用技术
- 电气元件制品的制造及其应用技术
- 发电;变电;配电装置的制造技术
- 电子电路装置的制造及其应用技术
- 电子通信装置的制造及其应用技术
- 其他产品的制造及其应用技术